Geometry in Text-to-Image Diffusion Models

Until recently, generative models were a bit like neural nets pre-2012 when AlexNet came out. People knew about them but kept asking what you could really use them for. Text-to-image models DALL-E and StableDiffusion, and the language model ChatGPT changed this–these models mark the AlexNet moment for generative modeling. The best part? These models are publicly available. So you can ask ChatGPT to tell a story while describing the scenery in detail every time it changes. Using a text-to-image model you can then translate that story into a movie¹, right? If this works, the movie will most likely contain changing cameras showing different parts of a 3D scene. As the camera moves, the scene might change according to the changing prompts used to generate the corresponding images. But will it work? Yes, kind of, but not out of the box, because these models do not have any mechanisms for generating 3D-consistent scenes. This blog will explore how we can use text-to-image models for generating 3D scenes–without retraining these models.

While no in-depth knowledge is required, it will be helpful to know what diffusion models and NeRF are. If you’d like to dig deeper, I recommend Sander Dieleman’s blog for an intro to diffusion models and a guide on how to make them conditional. For NeRF, check out the project website, and Frank Dellaert’s NeRF Explosion 2020 blog which provides a great overview of the history behind NeRF and its various extensions.

Coming back to stitching a movie from images: this is something you can use a text-to-image diffusion model for. Such image chaining is possible with diffusion models due to their ability to inpaint missing information (or to do image-to-image translation). We can just mask (think erase) a part of an image and ask a diffusion model to fill in the blank. The blank will generally be compatible with the unmasked parts of the image and the text prompt used to condition the model². See here for a cool demo of inpainting with StableDiffusion. This tutorial says a bit more about how StableDiffusion works and how inpainting is done. Note that if you can inpaint, you can also outpaint: by simply translating the image to the left, you can pretend that you masked the right side of the image (which is non-existent, but it doesn’t matter). The model will complete that right side of the image, effectively extending it.

So if you wanted to create an illusion of moving in a 3D scene represented by an image, you could just downscale that image (to move away) or upscale it (to move closer), and have the diffusion model fix any artifacts, right? The issue is that zooming out scales down everything the same way, but scaling as you move should depend on the distance from the camera (depth); Also you cannot walk forward, walk through doors, model occlusions or walk around and come back to the same place–the result would not be consistent with the previously-generated images. Here’s an example of what zooming out ad infinitum looks like.

To make the above work well, we would need to model not only the views of a given scene (images), but also the geometry (where things are, and where the camera that captured those views was). If we have the geometry, we can explicitly move the camera into a new position and capture the next image from there. If you can do this, you unlock a plethora of additional applications like generating whole scenes or 3D assets for virtual reality, computer games, or special effects in movies, for interior design, or any other artistic endeavor, really.

But building generative models of 3D scenes or objects is not easy. In my work, I focused on VAE-based generative models of NeRFs (NeRF-VAE and Laser-NV). In principle, these models offer very similar capabilities³. In practice, the quality of the generated 3D content is far far behind what text-to-image diffusion models generate these days. One reason is a different framework: GAUDI employs the diffusion modeling techniques used for image generation and applies them to 3D, which does result in better results than VAEs can provide. However, the model quality is still limited by the lack of high-quality 3D data.

While it is easy to scrape billions of images and associated text captions from the Internet, this isn’t the case for 3D. To do 3D modeling with NeRF (used in my work and in GAUDI above), you need several images and associated camera viewpoints for every scene, and, if you want to reach the scale of text-to-image models, you need millions if not billions of scenes in your dataset. This data does not exist on the Internet, because that’s not how people take (or post) pictures. Considering the scale, manually capturing such datasets is out of the question. The only respite is video, where different frames are captured from slightly different viewpoints, but video modeling opens up another can of worms: since the scene isn’t static, it is difficult to learn a scene representation that will be consistent across views (that preserves the geometry). The video diffusion models certainly do not offer multi-view consistency (Imagen Video, Make-a-Video). Nevertheless, video modeling with NeRF-based generative models is the most promising direction for future large-scale 3D models.

Text-to-Image Models Know About Geometry

But here’s the thing. We can play with the text-to-image models by manipulating the text prompt, which then shows that these models know about geometry. Perhaps the best example of this is DreamBooth.

If text-to-image models really know about 3D geometry, maybe we don’t need all that 3D data. Maybe we can just use the image models and either extract their 3D knowledge or perhaps somehow nudge them to preserve geometry across multiple generated images. It turns out that both approaches are possible, do not require re-training of the text-to-image models, and correspond to extracting geometry from an image model (DreamFusion and Score Jacobian Chaining (SJC)), and injecting geometry into an image model (SceneScape), respectively.

Extracting Geometry from an Image Model

Given that text-to-image diffusion models⁴ can generate pretty pictures and know about geometry, it is natural to ask if we can extract that geometry from these models. That is, can we lift a generated 2D picture to a full 3D scene? The answer is, of course, yes. But why does it work? Because any 2D rendering of a 3D representation is an image, and if that representation contains a scene familiar to the image model (i.e. in the model distribution), that rendered image should have a high likelihood under the image model. Conversely, if the represented scene is not familiar to the image model, the rendered image will have a low likelihood. Therefore, if we start from a random scene, the rendered images will have a low likelihood under the image model. But if we then manage to compute the gradients of the image model likelihood with respect to the 3D representation, we’ll be able to nudge the 3D representation into something that has a bit higher likelihood under that image model. Although they differ in derivations, both DreamFusion and SJC come up with novel image-space losses that capture the score (the derivative of the log probability) of a NeRF-rendered image under a pre-trained large-scale text-to-image diffusion model that is then back-propagated onto the NeRF parameters.

In theory, you don’t even have to use a diffusion model: any image model that can score a rendered image will do, including a VAE or any energy-based model including a GAN discriminator, a contrastive model such as CLIP or even a classifier. Check out DreamFields which uses CLIP to generate images and the DreamFusion and RealFusion papers (described below), which compare diffusion score against CLIP for training a NeRF. As Ben Poole pointed out, this may not work well in practice, since modes do not usually look like samples (see Sander’s blog on typicality), and likelihood from a VAE or EBM may fail in high dimensions.

The next few subsections describe technical details and follow-ups that are self-contained and not necessary for understanding the remainder of the blog. Feel free to skip some of them (but do take a look at the figures to see the results).

DreamFusion/SJC Algorithm

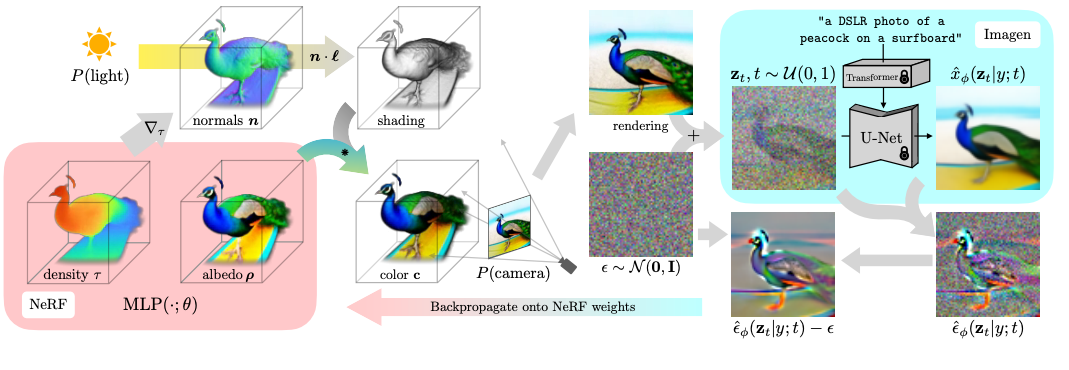
The simplified algorithm is as follows (the DreamFusion version):

1. Initialize a random NeRF and pick a text prompt for the diffusion model.
2. Pick a random camera pose.
3. Render an image at that camera pose using the NeRF.
4. Compute the score-matching loss under a pre-trained diffusion model.
5. Use the score-matching loss as a gradient with respect to the rendered image, and backpropagate it to NeRF’s parameters.
6. Go to step 2.

Of course, life is never that easy, and DreamFusion comes with several hacks, including changing the text prompt based on the sampled camera pose, clipping the scene represented by the NeRF to a small ball around the origin (any densities outside of the ball are set to zero), putting the rendered object on different backgrounds, additional losses that ensure e.g. that most of the space is unoccupied or that normals are well-behaved. Most of these tricks are designed to reveal bad learned geometry under the NeRF.e

Why Does Extracting Geometry Lead to Cartoonish Objects?

As you can see in the above examples, extracting geometry from image models can produce nice but cartoon-ish looking 3D models of single objects which are rather poor quality. You can get higher quality with heavily engineered approaches like Magic3D, but the algorithm is not as pretty.

Why does the simple version not work that well? While no one really knows, I have some theories. First, the 3D representation is initialized with a random NeRF, which leads to rendered images that look like random noise. In this case, the diffusion model will denoise each of these images towards a different image as opposed to different views of the same scene. This makes it difficult to get the optimization off the ground, which may lead to training instabilities and lower final quality. Second, this approach relies on classifier-free guidance with a very high guidance weight, which decreases the variance of the distribution (and its multimodality, see the end of this blog for a further discussion).

Why Only Objects? What Happened to Full 3D Scenes?

Beyond just the low-ish quality, the “scenes” generated by extracting geometry into a NeRF show single objects as opposed to full open-ended outdoor or indoor scenes. This is at least partly associated with the distribution of the cameras. If you are trying to model a general 3D scene (a part of a city or an apartment), the distribution of viable cameras is tightly coupled to the layout of the scene. In an apartment, say, randomly sampling cameras will yield cameras that are within walls and other objects. This will result in an empty image, which is unlikely under the model. Optimization in such a case will lead to removing any objects that occlude the scene from the camera: in this case, it will remove everything, resulting in an empty scene. This is precisely why GAUDI models the joint distribution of indoor scenes and camera distributions (private correspondence with the authors).

View-Conditioned Follow-ups

Next, I’d like to describe RealFusion and NerfDiff: two different takes at extracting geometry from a diffusion model but in such a way that extracted geometry (NeRF) is consistent with a provided image. RealFusion is a view-conditioned version of DreamFusion. It does everything that DreamFusion does, but instead of a vanilla text-to-image diffusion model, the authors use DreamBooth to constrain the diffusion model to a specific object shown by a target image. In addition to forcing the NeRF to represent that object, it should result in lower-variance gradients for the NeRF and therefore better NeRF quality.

NerfDiff is similar, but instead of fitting a NeRF from scratch, the authors train a view-conditioned (amortized) NeRF. Another difference is that instead of using a pretrained text-to-image diffusion model, NerfDiff fits a custom view-conditioned (not text-conditioned) diffusion model jointly with the amortized NeRF on the target dataset of scenes. Why? Because diffusion models tend to achieve much better image quality than amortized NeRFs at the cost of not being consistent across different views. The amortized NeRF allows a fast NeRF initialization from a single image, which is then fine-tuned with distillation from the diffusion model. The authors also introduce a novel distillation algorithm that improves on DreamFusion/SJC quite a bit (but is quite a bit more expensive). NerfDiff can produce NeRFs only from images that are similar to the training images; RealFusion doesn’t have this issue because it uses a pretrained large-scale diffusion model.

Injecting Geometry into an Image Model

This idea is almost the polar opposite: instead of distilling geometry from the image model and putting it somewhere else, we will use our understanding of 3D geometry to guide the image model to generate images that look like they represent the same scene but are generated from different camera poses.

The main insight behind the SceneScape algorithm is that an image diffusion model can correct image imperfections with its superb inpainting abilities. Now imagine that we have an image captured from a given camera position, and we pretend to move to a different camera position. Can you imagine how that image would look from the new viewpoint? You will mostly see the same things, just from a different distance and angle; some things will now be missing, and you will see some parts of the scene that you were not able to see before. It turns out that you can do this operation analytically by warping the original image into the new viewpoint. Warping results in an imperfect image:

• Specularities and other view-dependent lighting effects will be incorrect.
• It will have holes because not everything was observed.

But mostly, the image will look ok. The diffusion model can fill in the holes, and possibly even fix the lighting artifacts: there you go, we just created a new image, taken from a different camera position, that is geometrically consistent (distances are respected) and semantically consistent (the things visible in the first image are still there and are the same). The best part? We used an off-the-shelf pretrained image model. It doesn’t even have to be a diffusion model: all we need is the inpainting ability.

Technical: SceneScape Algorithm

A naive version of the SceneScape algorithm requires:

• a pretrained text-to-image diffusion model capable of inpainting missing values,
• a pretrained depth-from-a-single-image predictor (required for warping (above) or mesh building (below)),
• a text prompt,
• and optionally an image to start from,
• and a method to infer intrinsic camera parameters for an RGBD image.

We then do the following:

1. Generate an initial image (or use the one you want to start with). Initialize the camera position and orientation to an arbitrary value.
2. Predict the depth for that image.
3. Infer intrinsics for the RGBD image that you now have. You will only have to do this once as hopefully, the diffusion model will preserve the camera parameters when inpainting missing values.
4. Change the camera position and orientation.
5. Project the previously-generated RGBD images onto the new camera pose (this is where intrinsics come into play). It will contain holes.
6. Feed the projected RGB image into the diffusion model and fill in any missing values. Go to step 2.

In the paper, the authors start by generating an image from a text prompt. Camera intrinsics are necessary to render previously-generated RGBD images onto a new camera position. The paper assumes just an arbitrary fixed camera model, which introduces errors, but apparently the diffusion model is able to fix that, too. I augmented the algorithm a little to allow starting from a real image and to reduce the reprojection errors from incorrect camera intrinsics.

Only it turns out that there are rough edges that need to be smoothed out (as done in the paper):

• Reprojection from previously captured RGBD images is not great and is much better done by building a mesh as a global scene representation.
• The depth predicted from single images is inconsistent across the images (the differences between depth do not respect the changes in camera position), so the authors fine-tune the depth predictor: after projecting the mesh on a new camera they fine-tune the depth predictor to agree with the depth that came out from that projection. Once the depth predictor agrees with the mesh, we can predict the values for the holes in the depth map. This requires optimization of the depth predictor at every generated frame. The authors don’t mention how many gradient steps it takes.
• The authors use StableDiffusion as their text-to-image model, which is a Latent Diffusion model operating on embeddings of a VAE trained with perceptual and adversarial losses. Since the VAE did not optmize reconstruction error, autoencoding results in somewhat low reconstruction quality. Therefore, to reconstruct an image that fits visually with previously-observed frame, the authors need to finetune the VAE decoder to improve its reconstruction quality. Similarly to the depth predictor, they first optimize it so that it agrees on these parts of the image that are reprojected from the mesh and then use the finetuned decoder to fill in any holes (RGB and depth will have the same holes).
• Lastly, the inpainted part of the frame may not agree semantically with the text prompt very well; they generate multiple frames and then use cosine distance between the CLIP embeddings of the text and the generated frames to choose the frame that is best aligned with the prompt.

Limitations:

• The mesh representation doesn’t work well for outdoor scenes (depth discontinuities between objects and the sky).
• There is error accumulation in long generated sequences that sometimes lead to less-than-realistic results.

While not stated in the paper, Rafail mentioned that they finetune the depth predictor and the VAE decoder for 300 and 100 gradients steps, respectively. It takes about an hour to generate 50 frames on a Tesla V100.

Why is it important for the image model to be text conditioned?

I left this discussion until after describing the two approaches of extracting and injecting geometry because it requires understanding some technical details about how these methods work.

Generally speaking, modeling conditional probability distributions is easier than modeling unconditional ones. This may seem counter-intuitive at first, because to modal a conditional probability \(p(x \mid z)\) you have to learn the relationship between \(x\) and \(z\), which you don’t have to do if you are modeling just \(p(x)\). While that is true, \(p(x)\) is generally a much more complicated object than \(p(x \mid z)\). To see this, look at a Gaussian mixture with K components. In this case, to recover the true \(p(x)\) with a learned \(\widetilde{p}(x)\), we have to parametrize \(\widetilde{p}(x)\) with a family of distributions expressive enough to cover the 10 different modes. If, however, we model the conditional \(p(x \mid z)\) where \(z\) now is an index telling us which mode we care about, the learned \(\widetilde{p}(x \mid z)\) has to model just one mode at a time. In this example, it can be just a Gaussian. A larger-scale example is that of ImageNet with 1000 different classes. In that case, you can think of the data distribution as a mixture of 1000 components, but now the components are very high-dimensional (images of shape 224x224x3), and the individual components are highly non-Gaussian, so the problem is much more difficult. Modeling conditionals in this case is way simpler.

So what does this have to do with image models and geometry?

I did some experiments with a DreamFusion-like setup, where I played with an unconditional and a view-conditional image model trained from scratch on a smaller dataset. It turns out that if the image model is unconditional, the gradients that it produces to train the NeRF point in a multitude of different directions. What happens in practice is that the NeRF initially starts to represent a scene, but eventually that scene disappears and the NeRF represents just empty space. This changes when we introduce conditioning: either a text prompt describing an object (like in DreamFusion or SJC), or an image (like in RealFusion or NerfDiff). The bottom line: too many modes lead to too high a variance of the gradients used to train the NeRF. Decreasing the number of modes leads to better-behaved gradients and thus learning.

A very similar argument applies to injecting geometry into an image model. One of the limitations of SceneScape is the accumulation of errors. This is partly mitigated by generating more than just one inpainting of the image from a new camera position, and then choosing the one that best aligns with the text prompt under CLIP similarity. So if the distribution of the image model had many more modes (if it was unconditional), it would be much more likely to inpaint missing parts of the image in a way that is not very consistent with the presented image, leading to faster error accumulation. If the model wasn’t text-conditioned, the authors couldn’t have done the CLIP trick of choosing the most suitable image in the first place, which would have significantly exacerbated the error accumulation.

So we see that the ability to model insanely complex distributions (unconditional distributions of real images) is counter-productive. Perhaps that’s ok because whenever we want to generate an image, we would like to have some control over what we’re generating. However, this suggests a future failure case. As the generative models get bigger, more expressive, and trained on more data, they will represent distributions with more and more modes. This is true even for conditional models. Does it mean that, with the advances in generative modeling, the approaches of injecting and extracting geometry (and anything that requires constraining the variance of the distribution) will stop working? As with anything, there will be workarounds. But it’s an interesting failure case to keep in mind.

Conclusions

While I’m not sure what I said with this blog, what I wanted to say is this⁵. There is value in making generative models. Ideally, we would be able to train such models on large datasets of 3D assets, or from videos. But this is difficult because there isn’t enough 3D data, and modeling videos while also modeling the geometry of the underlying scenes is tricky. So if it suits your application, why not try a simpler approach? Maybe you can take an off-the-shelf text-to-image diffusion model, and then massage it a bit so that it gives you a 3D model instead of just a 2D image. There you go.

Acknowledgements

I would like to thank Heiko Strathmann and Danilo J. Rezende for numerous discussions about topics covered in this blog. I also thank Jimmy Shi, Hyunjik Kim, Leonard Hasenclever, Adam Goliński, and Heiko for feedback on an initial version of this post.

Also thanks to Rafail Fridman and Ben Poole who provided feedback on the SceneScape and DreamFusion coverage in this blog, respectively.

Footnotes